Como inventor del álgebra de Boole, que marca los fundamentos de la aritmética computacional moderna, Boole es considerado como uno de los fundadores del campo de las Ciencias de la Computación. En 1854 publicó An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities,
donde desarrolló un sistema de reglas que le permitían expresar,
manipular y simplificar problemas lógicos y filosóficos cuyos argumentos
admiten dos estados (verdadero o falso) por procedimientos matemáticos.
Se podría decir que es el padre de las operaciones lógicas y gracias a
su álgebra hoy en día es posible manipular operaciones lógicas.

En informática y matemática, es una estructura algebraica que esquematiza las operaciones lógicas Y, O, NO y SI (AND, OR, NOT, IF), así como el conjunto de operaciones unión, intersección y complemento.
-
 Dado un conjunto:
Dado un conjunto: 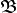 formado cuando menos por los elementos:
formado cuando menos por los elementos: 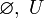 en el que se ha definido:
en el que se ha definido:- Una operación unaria interna, que llamaremos complemento:
- La operación binaria interna, que llamaremos suma:
- La operación binaria interna, que llamaremos producto:
Dada la definición del álgebra de Boole como una estructura algebraica genérica, según el caso concreto de que se trate, la simbología y los nombres de las operaciones pueden variar.
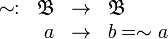



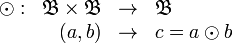

No hay comentarios:
Publicar un comentario